Preamble
import numpy as np # for multi-dimensional containers
import pandas as pd # for DataFrames
import plotly.graph_objects as go # for data visualisation
Introduction
In mathematics, optimisation is concerned with the selection of optimal solutions to objective functions. An objective function consists of input arguments referred to as problem variables (or genotype) which are computed by one or many mathematical functions to determine the objective value (or phenotype).
Real-world optimisation problems are divided into one (in the case of single-objective optimisation) or many (in the case of multi-objective optimisation) objective functions in order to be optimised by an optimisation algorithm. The difficulty of convergence can be reduced by the bounding of problem variables as this reduces the size of the search domain.
In order to determine an Evolutionary Algorithm's robustness when solving problems consisting of multiple objectives, its performance must be assessed on the optimisation of synthetic test functions which are created for the purpose of testing. These problems may also be used to systematically compare two or more Evolutionary Algorithms.
Synthetic test functions are typically:
- Intentionally difficult, meaning they are designed to include optimisation difficulties which are present in real-world problems.
- Scalable, meaning they can be configured with a different number of problem variables and objectives.
- Computationally efficient, meaning they are faster to execute than a real-world problem. This is desirable when benchmarking an Evolutionary Algorithm.
In contrast, real-world problems which have been encapsulated within an objective function in order to be used by an optimiser are often computationally expensive and have long execution times. This is because synthetic test functions are often mathematical equations which aim to cause difficulty for an optimiser when searching for problem variables that produce optimal objective values, whereas real-world problems often involve computationally expensive simulations in order to arrive at the objective values.
Put simply, using a real-world problem to evaluate the performance of a newly proposed Evolutionary Algorithm only allows us to determine if an algorithm is good at solving that single problem. What we're interested in is analysing how Evolutionary Algorithms perform when encountering various difficulties that appear in multi-objective problems, and how they compare to each other.
The ZDT1 test function
We will be using a synthetic test problem throughout this notebook called ZDT1. It is part of the ZDT test suite, consisting of six different two-objective synthetic test problems. This is quite an old test suite, easy to solve, and very easy to visualise.
Mathematically, the ZDT11 two-objective test function can be expressed as:
where
and all decision variables fall between
For this bi-objective test function,
Let's start implementing this in Python, beginning with the initialisation of a solution according to Equations 2 and 3. In this case, we will have 30 problem variables
D = 30
x = np.random.rand(D)
print(x)
[0.5790907 0.44812092 0.13563843 0.38454285 0.22041174 0.53338134 0.61942627 0.13298216 0.03642106 0.1588064 0.0594002 0.50837213 0.60625198 0.63383043 0.87137317 0.01786989 0.73270498 0.64518276 0.25394609 0.30109357 0.46625086 0.0788334 0.86954539 0.73028488 0.31167315 0.56357543 0.29216487 0.93692486 0.02998881 0.20909433]
Now that we have a solution to evaluate, let's implement the ZDT1 synthetic test function using Equation 1.
def ZDT1(x):
f1 = x[0] # objective 1
g = 1 + 9 * np.sum(x[1:D] / (D - 1))
h = 1 - np.sqrt(f1 / g)
f2 = g * h # objective 2
return [f1, f2]
Finally, let's invoke our implemented test function using our solution
objective_values = ZDT1(x)
print(objective_values)
[0.5790906971991833, 3.015929957969631]
Now we can see the two objective values that measure our solution
Performance in Objective Space
We will be discussing desirable characteristics in multi-objective solutions, but for now, let's plot some randomly initialised solutions against an optimal set of solutions for ZDT1. This is a synthetic test function, and as such the authors have provided us with a way to calculate the optimal set.
Let's use this to generate 20 ideal sets of objective values.
true_front = np.empty((0, 2))
for f1 in np.linspace(0, 1, num=20):
f2 = 1 - np.sqrt(f1)
true_front = np.vstack([true_front, [f1, f2]])
# convert to DataFrame
true_front = pd.DataFrame(true_front, columns=["f1", "f2"])
true_front
| f1 | f2 | |
|---|---|---|
| 0 | 0.000000 | 1.000000 |
| 1 | 0.052632 | 0.770584 |
| 2 | 0.105263 | 0.675557 |
| 3 | 0.157895 | 0.602640 |
| 4 | 0.210526 | 0.541169 |
| 5 | 0.263158 | 0.487011 |
| 6 | 0.315789 | 0.438049 |
| 7 | 0.368421 | 0.393023 |
| 8 | 0.421053 | 0.351114 |
| 9 | 0.473684 | 0.311753 |
| 10 | 0.526316 | 0.274524 |
| 11 | 0.578947 | 0.239114 |
| 12 | 0.631579 | 0.205281 |
| 13 | 0.684211 | 0.172830 |
| 14 | 0.736842 | 0.141605 |
| 15 | 0.789474 | 0.111477 |
| 16 | 0.842105 | 0.082337 |
| 17 | 0.894737 | 0.054095 |
| 18 | 0.947368 | 0.026671 |
| 19 | 1.000000 | 0.000000 |
Now we can plot them to have an idea of the shape of the true front for ZDT1 in objective space.
fig = go.Figure(layout=dict(xaxis=dict(title="f1"), yaxis=dict(title="f2")))
fig.add_scatter(x=true_front.f1, y=true_front.f2, mode="markers")
fig.show()
To wrap things up, let's generate 50 objective values using the ZDT1 objective function created above. We achieve this by passing in 50 randomly initialised sets of problem variables.
objective_values = np.empty((0, 2))
for i in range(50):
x = np.random.rand(D)
y = ZDT1(x)
objective_values = np.vstack([objective_values, y])
# convert to DataFrame
objective_values = pd.DataFrame(objective_values, columns=["f1", "f2"])
objective_values.head()
| f1 | f2 | |
|---|---|---|
| 0 | 0.955349 | 2.726233 |
| 1 | 0.342559 | 4.077294 |
| 2 | 0.463095 | 3.915386 |
| 3 | 0.481782 | 3.617730 |
| 4 | 0.422303 | 3.404079 |
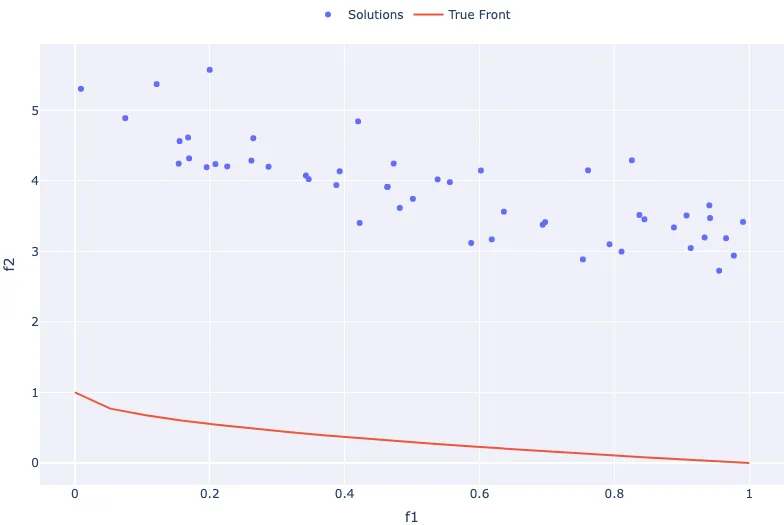
Now we will plot the objective values of our randomly initialised solutions on top of a plot of the true front, this will give us some idea of the difference in performance between the two sets.
fig = go.Figure(layout=dict(xaxis=dict(title="f1"), yaxis=dict(title="f2")))
fig.add_scatter(
x=objective_values.f1,
y=objective_values.f2,
name="Solutions",
mode="markers",
)
fig.add_scatter(x=true_front.f1, y=true_front.f2, name="True Front")
fig.show()
Conclusion
In this section, we introduced the concept of synthetic test functions along with ZDT1, a popular and relatively easy example. We expressed the concept mathematically and then made a direct implementation using Python. We then generated a set of 50 solutions, calculated the objective values for each one, and plotted the objective space using a scatter plot.
There are many suites of synthetic test functions in the literature, some to read about are ZDT, DTLZ, CEC09, and WFG Toolkit.
Exercise
Using the ZDT test suite paper listed in the references, duplicate this notebook but with the focus on ZDT2 instead of ZDT1.
-
E. Zitzler, K. Deb, and L. Thiele. Comparison of Multiobjective Evolutionary Algorithms: Empirical Results. Evolutionary Computation, 8(2):173-195, 2000 ↩