Preamble
import itertools
import pandas as pd # for DataFrames
from plotapi import Chord
Introduction
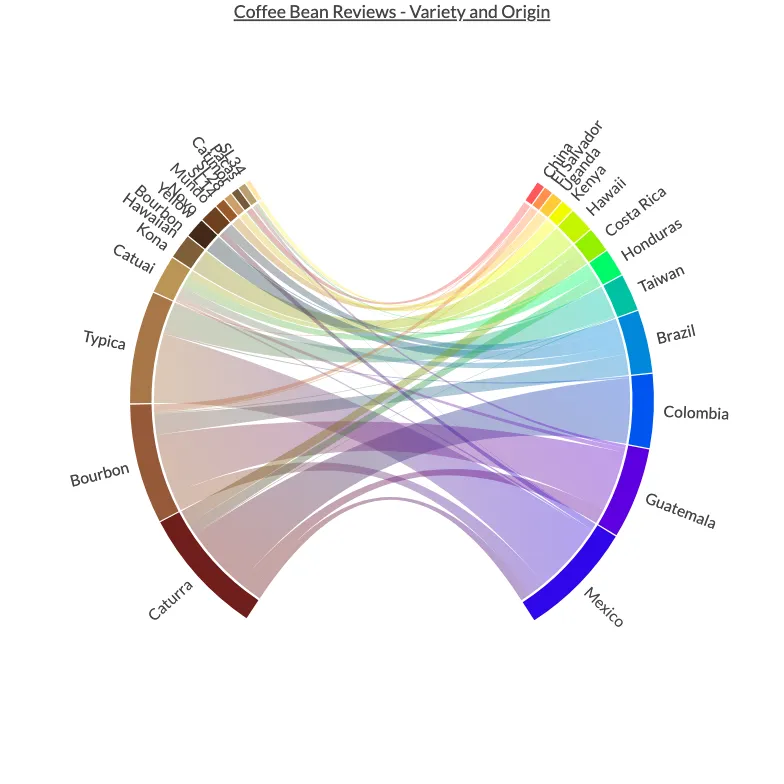
In this section, we're going to be pointing our beautifully colourful lens towards the warm and aromatic world of coffee. In particular, we're going to be visualising the co-occurrence of coffee bean variety and origin in over a thousand coffee reviews.
Note
This section uses the PlotAPI software to create a visualisation. Check out the link to produce the same output!
The Dataset
We're going to use the popular Coffee Quality Institute Database which I have forked on GitHub for posterity. The file arabatica_data.csv contains the data we'll be using throughout this section, and the first thing we'll want to do is to load the data and output some samples for a sanity check.
data = pd.read_csv("https://datacrayon.com/datasets/arabica_data.csv")
data.head()
| Unnamed: 0 | Species | Owner | Country.of.Origin | Farm.Name | Lot.Number | Mill | ICO.Number | Company | Altitude | ... | Color | Category.Two.Defects | Expiration | Certification.Body | Certification.Address | Certification.Contact | unit_of_measurement | altitude_low_meters | altitude_high_meters | altitude_mean_meters | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | Arabica | metad plc | Ethiopia | metad plc | NaN | metad plc | 2014/2015 | metad agricultural developmet plc | 1950-2200 | ... | Green | 0 | April 3rd, 2016 | METAD Agricultural Development plc | 309fcf77415a3661ae83e027f7e5f05dad786e44 | 19fef5a731de2db57d16da10287413f5f99bc2dd | m | 1950.0 | 2200.0 | 2075.0 |
| 1 | 2 | Arabica | metad plc | Ethiopia | metad plc | NaN | metad plc | 2014/2015 | metad agricultural developmet plc | 1950-2200 | ... | Green | 1 | April 3rd, 2016 | METAD Agricultural Development plc | 309fcf77415a3661ae83e027f7e5f05dad786e44 | 19fef5a731de2db57d16da10287413f5f99bc2dd | m | 1950.0 | 2200.0 | 2075.0 |
| 2 | 3 | Arabica | grounds for health admin | Guatemala | san marcos barrancas "san cristobal cuch | NaN | NaN | NaN | NaN | 1600 - 1800 m | ... | NaN | 0 | May 31st, 2011 | Specialty Coffee Association | 36d0d00a3724338ba7937c52a378d085f2172daa | 0878a7d4b9d35ddbf0fe2ce69a2062cceb45a660 | m | 1600.0 | 1800.0 | 1700.0 |
| 3 | 4 | Arabica | yidnekachew dabessa | Ethiopia | yidnekachew dabessa coffee plantation | NaN | wolensu | NaN | yidnekachew debessa coffee plantation | 1800-2200 | ... | Green | 2 | March 25th, 2016 | METAD Agricultural Development plc | 309fcf77415a3661ae83e027f7e5f05dad786e44 | 19fef5a731de2db57d16da10287413f5f99bc2dd | m | 1800.0 | 2200.0 | 2000.0 |
| 4 | 5 | Arabica | metad plc | Ethiopia | metad plc | NaN | metad plc | 2014/2015 | metad agricultural developmet plc | 1950-2200 | ... | Green | 2 | April 3rd, 2016 | METAD Agricultural Development plc | 309fcf77415a3661ae83e027f7e5f05dad786e44 | 19fef5a731de2db57d16da10287413f5f99bc2dd | m | 1950.0 | 2200.0 | 2075.0 |
5 rows × 44 columns
Data Wrangling
By viewing the CSV directly we can see our desired columns are named Country.of.Origin and Variety. Let's print out the columns to make sure they exist in the data we've loaded.
data.columns
Index(['Unnamed: 0', 'Species', 'Owner', 'Country.of.Origin', 'Farm.Name',
'Lot.Number', 'Mill', 'ICO.Number', 'Company', 'Altitude', 'Region',
'Producer', 'Number.of.Bags', 'Bag.Weight', 'In.Country.Partner',
'Harvest.Year', 'Grading.Date', 'Owner.1', 'Variety',
'Processing.Method', 'Aroma', 'Flavor', 'Aftertaste', 'Acidity', 'Body',
'Balance', 'Uniformity', 'Clean.Cup', 'Sweetness', 'Cupper.Points',
'Total.Cup.Points', 'Moisture', 'Category.One.Defects', 'Quakers',
'Color', 'Category.Two.Defects', 'Expiration', 'Certification.Body',
'Certification.Address', 'Certification.Contact', 'unit_of_measurement',
'altitude_low_meters', 'altitude_high_meters', 'altitude_mean_meters'],
dtype='object')Great! We can see both of these columns exist in our DataFrame.
Now let's take a peek at the unique values in both of these columns to see if any obvious issues stand out. We'll start with the Country.of.Origin column.
data["Country.of.Origin"].unique()
array(['Ethiopia', 'Guatemala', 'Brazil', 'Peru', 'United States',
'United States (Hawaii)', 'Indonesia', 'China', 'Costa Rica',
'Mexico', 'Uganda', 'Honduras', 'Taiwan', 'Nicaragua',
'Tanzania, United Republic Of', 'Kenya', 'Thailand', 'Colombia',
'Panama', 'Papua New Guinea', 'El Salvador', 'Japan', 'Ecuador',
'United States (Puerto Rico)', 'Haiti', 'Burundi', 'Vietnam',
'Philippines', 'Rwanda', 'Malawi', 'Laos', 'Zambia', 'Myanmar',
'Mauritius', 'Cote d?Ivoire', nan, 'India'], dtype=object)We can see some points that may cause issues when it comes to our visualisation.
There appears to be at least one nan value in Country.of.Origin. We're only interested in coffee bean reviews which aren't missing this data, so let's remove any samples where nan exists.
data = data[data["Country.of.Origin"].notna()]
Also, the entries in Country.of.Origin will be used as labels on our visualisation. Ideally, we don't want these to be longer than they need to be. So let's shorten some of the longer names.
data["Country.of.Origin"] = data["Country.of.Origin"].replace(
"United States (Hawaii)", "Hawaii"
)
data["Country.of.Origin"] = data["Country.of.Origin"].replace(
"Tanzania, United Republic Of", "Tanzania"
)
data["Country.of.Origin"] = data["Country.of.Origin"].replace(
"United States (Puerto Rico)", "Puerto Rico"
)
Now let's take a peek at the unique Variety column.
data["Variety"].unique()
array([nan, 'Other', 'Bourbon', 'Catimor', 'Ethiopian Yirgacheffe',
'Caturra', 'SL14', 'Sumatra', 'SL34', 'Hawaiian Kona',
'Yellow Bourbon', 'SL28', 'Gesha', 'Catuai', 'Pacamara', 'Typica',
'Sumatra Lintong', 'Mundo Novo', 'Java', 'Peaberry', 'Pacas',
'Mandheling', 'Ruiru 11', 'Arusha', 'Ethiopian Heirlooms',
'Moka Peaberry', 'Sulawesi', 'Blue Mountain', 'Marigojipe',
'Pache Comun'], dtype=object)We can see this column also has at least one nan entry, so let's remove these too.
data = data[data["Variety"].notna()]
Also, there appears to be at least one entry of Other for the Variety. For this visualisation, we're not interested in Other, so let's remove them too.
data = data[data["Variety"] != "Other"]
From previous Chord diagram visualisations we know that they can become too crowded with too many different categories. With this in mind, let's choose to visualise only the top Country.of.Origin and Variety.
data = data[
data["Country.of.Origin"].isin(
list(data["Country.of.Origin"].value_counts()[:12].index)
)
]
data = data[
data["Variety"].isin(list(data["Variety"].value_counts()[:12].index))
]
As we're creating a bipartite chord diagram, let's define what labels will be going on the left and the right.
On the left, we'll have all of our countries of origin.
left = list(data["Country.of.Origin"].value_counts().index)[::-1]
pd.DataFrame(left)
| 0 | |
|---|---|
| 0 | China |
| 1 | El Salvador |
| 2 | Uganda |
| 3 | Kenya |
| 4 | Hawaii |
| 5 | Costa Rica |
| 6 | Honduras |
| 7 | Taiwan |
| 8 | Brazil |
| 9 | Colombia |
| 10 | Guatemala |
| 11 | Mexico |
And on the right, we'll have all of our varieties.
right = list(data["Variety"].value_counts().index)
pd.DataFrame(right)
| 0 | |
|---|---|
| 0 | Caturra |
| 1 | Bourbon |
| 2 | Typica |
| 3 | Catuai |
| 4 | Hawaiian Kona |
| 5 | Yellow Bourbon |
| 6 | Mundo Novo |
| 7 | SL14 |
| 8 | SL28 |
| 9 | Catimor |
| 10 | Pacas |
| 11 | SL34 |
We're good to go! So let's select just these two columns and work with a DataFrame containing only them as we move forward.
origin_variety = pd.DataFrame(data[["Country.of.Origin", "Variety"]].values)
origin_variety
| 0 | 1 | |
|---|---|---|
| 0 | Guatemala | Bourbon |
| 1 | China | Catimor |
| 2 | Costa Rica | Caturra |
| 3 | Brazil | Bourbon |
| 4 | Uganda | SL14 |
| ... | ... | ... |
| 884 | Honduras | Catuai |
| 885 | Honduras | Catuai |
| 886 | Mexico | Bourbon |
| 887 | Guatemala | Catuai |
| 888 | Honduras | Caturra |
889 rows × 2 columns
Our chord diagram will need two inputs: the co-occurrence matrix, and a list of names to label the segments.
We can build this list of names by adding together the labels for the left and right side of our bipartite diagram.
names = left + right
pd.DataFrame(names)
| 0 | |
|---|---|
| 0 | China |
| 1 | El Salvador |
| 2 | Uganda |
| 3 | Kenya |
| 4 | Hawaii |
| 5 | Costa Rica |
| 6 | Honduras |
| 7 | Taiwan |
| 8 | Brazil |
| 9 | Colombia |
| 10 | Guatemala |
| 11 | Mexico |
| 12 | Caturra |
| 13 | Bourbon |
| 14 | Typica |
| 15 | Catuai |
| 16 | Hawaiian Kona |
| 17 | Yellow Bourbon |
| 18 | Mundo Novo |
| 19 | SL14 |
| 20 | SL28 |
| 21 | Catimor |
| 22 | Pacas |
| 23 | SL34 |
Now we can create our empty co-occurrence matrix using these type names for the row and column indeces.
matrix = pd.DataFrame(0, index=names, columns=names)
matrix
| China | El Salvador | Uganda | Kenya | Hawaii | Costa Rica | Honduras | Taiwan | Brazil | Colombia | ... | Typica | Catuai | Hawaiian Kona | Yellow Bourbon | Mundo Novo | SL14 | SL28 | Catimor | Pacas | SL34 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| China | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| El Salvador | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Uganda | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Kenya | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Hawaii | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Costa Rica | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Honduras | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Taiwan | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Brazil | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Colombia | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Guatemala | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Mexico | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Caturra | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bourbon | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Typica | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Catuai | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Hawaiian Kona | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Yellow Bourbon | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Mundo Novo | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SL14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SL28 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Catimor | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Pacas | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SL34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
24 rows × 24 columns
We can populate a co-occurrence matrix with the following approach. We'll start by creating a list with every type pairing in its original and reversed form.
origin_variety = list(
itertools.chain.from_iterable(
(i, i[::-1]) for i in origin_variety.values
)
)
Which we can now use to create the matrix.
for pairing in origin_variety:
matrix.at[pairing[0], pairing[1]] += 1
matrix = matrix.values.tolist()
We can list the DataFrame for better presentation.
pd.DataFrame(matrix)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 17 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 14 | 0 | 0 | 8 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 44 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 21 | 0 | 0 | 0 | 0 | 0 | 1 | 4 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 59 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 19 | 0 | 32 | 20 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 137 | 4 | 0 | 0 | 12 | 0 | 0 | 0 | 1 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 28 | 23 | 2 | 0 | 129 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13 | 0 | 13 | 3 | 0 | 0 | 1 | 0 | 2 | 41 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 59 | 0 | 3 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 15 | 0 | 0 | 0 | 0 | 0 | 15 | 21 | 0 | 19 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 16 | 0 | 0 | 0 | 0 | 44 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 32 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 19 | 0 | 0 | 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | 0 | 0 | 0 | 14 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 21 | 12 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 22 | 0 | 2 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 23 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
24 rows × 24 columns
Chord Diagram
Time to visualise the co-occurrence of items using a chord diagram. We are going to use a list of custom colours that represent the items.
Let's specify some colours for the left and right sides.
colors = [
"#ff575c","#ff914d","#ffca38","#f2fa00","#C3F500","#94f000",
"#00fa68","#00C1A2","#0087db","#0054f0","#5d00e0","#2F06EB",
"#6f1d1b","#955939","#A87748","#bb9457","#7f5e38","#432818",
"#6e4021","#99582a","#cc9f69","#755939","#BAA070","#ffe6a7"]
Finally, we can put it all together using PlotAPI Chord.
Chord(
matrix,
names,
colors=colors,
width=900,
padding=0.01,
font_size=12,
font_size_large=16,
noun="coffee bean reviews",
title="Coffee Bean Reviews - Variety and Origin",
bipartite=True,
bipartite_idx=len(left),
bipartite_size=0.6,
allow_download=True,
)
Conclusion
In this section, we demonstrated how to conduct some data wrangling on a downloaded dataset to prepare it for a bipartite chord diagram. Our chord diagram is interactive, so you can use your mouse or touchscreen to investigate the co-occurrences!