Preamble
import numpy as np # for multi-dimensional containers
import pandas as pd # for DataFrames
import plotly.graph_objects as go # for data visualisation
from plotly.subplots import make_subplots
import scipy.fftpack # discrete Fourier transforms
In a previous section we looked at how to create a single Sine Wave and visualise it in the time domain.
sample_rate = 1000
start_time = 0
end_time = 10
time = np.arange(start_time, end_time, 1/sample_rate)
frequency = 3
amplitude = 1
theta = 0
sinewave = amplitude * np.sin(2 * np.pi * frequency * time + theta)
fig = go.Figure(layout=dict(xaxis=dict(title='Time (sec)'),yaxis=dict(title='Amplitude')))
fig.add_scatter(x=time, y=sinewave)
fig.show()
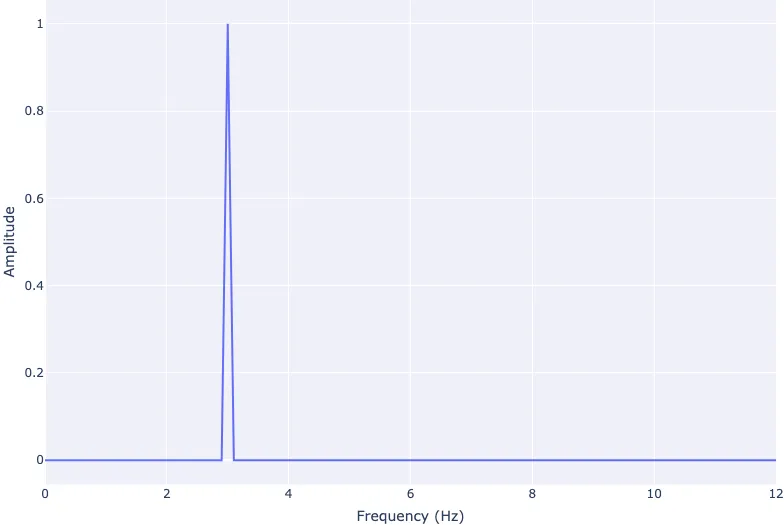
Fourier Transform
freq = scipy.fftpack.fft(sinewave)/len(time)
hz = np.linspace(0, sample_rate/2, int(np.floor(len(time)/2)+1))
fig = go.Figure(
layout=dict(
xaxis=dict(title='Frequency (Hz)', range=[0, np.max(frequency) * 1.2]),
yaxis=dict(title='Amplitude'))
)
fig.add_scatter(x=hz, y=2 * np.abs(freq))
fig.show()
Summing Sine Waves
sample_rate = 1000
start_time = 0
end_time = 10
theta = 0
time = np.arange(start_time, end_time, 1/sample_rate)
frequency = [3, 5, 2, 1, 10]
amplitude = [1, 2, 7, 3, 0.1]
fig = go.Figure(layout=dict(xaxis=dict(title='Time (sec)'),yaxis=dict(title='Amplitude')))
fig.add_scatter(x=time, y=sinewave)
fig.show()
fig = go.Figure(layout=dict(xaxis=dict(title='Time (sec)'),yaxis=dict(title='Amplitude')))
fig.add_scatter(x=time, y=sinewave)
fig.show()
freq = scipy.fftpack.fft(sinewave)/len(time)
hz = np.linspace(0, sample_rate/2, int(np.floor(len(time)/2)+1))
fig = go.Figure(
layout=dict(
xaxis=dict(title='Frequency (Hz)', range=[0, np.max(frequency) * 1.2]),
yaxis=dict(title='Amplitude'))
)
fig.add_scatter(x=hz, y=2 * np.abs(freq))
fig.show()