In this article we're going to introduce the problem of dataset class imbalance which often occurs in real-world classification problems. We'll then look at oversampling as a possible solution and provide a coded example as a demonstration on an imbalanced dataset.
Class imbalance
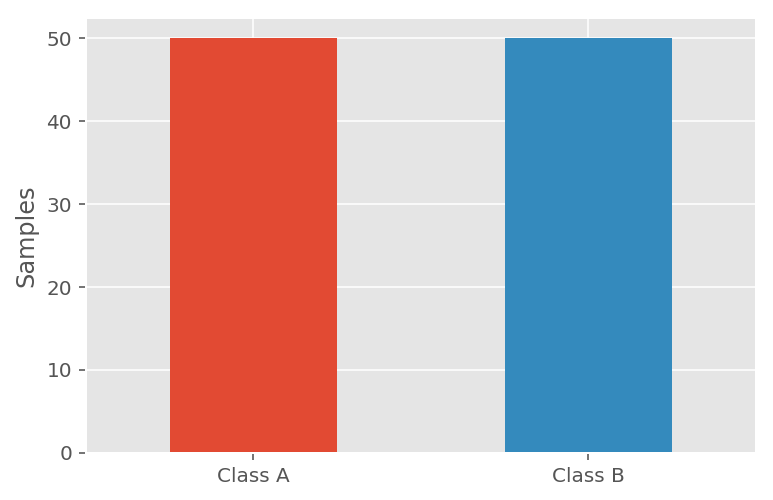
Let's assume we have a dataset where the data points are classified into two categories: Class A and Class B. In an ideal scenario the division of the data point classifications would be equal between the two categories, e.g.:
- Class A accounts for 50% of the dataset.
- Class B accounts for the other 50% of the dataset.
With the above scenario we could sufficiently measure the performance of a classification model using classification accuracy.
Unfortunately, this ideal balance often isn't the case when working with real-world problems, e.g. where categories of interest may occur less often. For context, here are some examples:
- Credit Card Fraud : The majority of credit card transactions are genuine, whereas the minority of credit card transactions are fraudulent.
- Medical Scans : The majority of medical scans are normal, whereas the minority of medical scans indicate something pathological.
- Weapons Detection: The majority of body scans are normal, whereas the minority of body scans detect a concealed weapon.
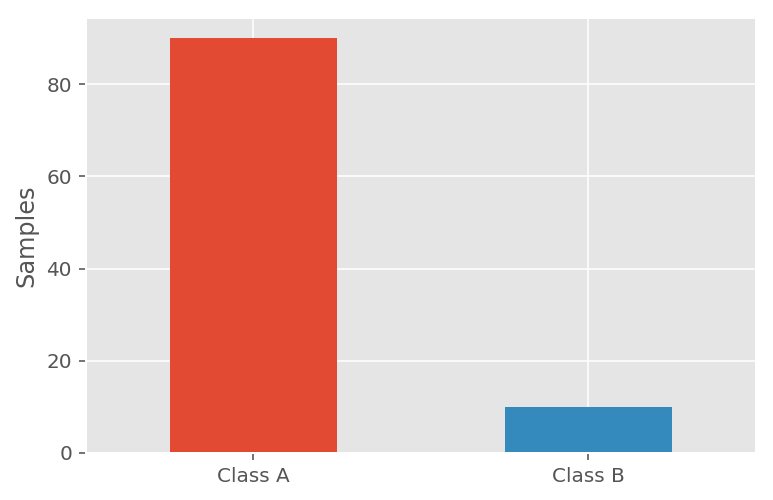
An imbalanced dataset could consist of data points divided as follows:
- Class A accounts for 90% of the dataset.
- Class B accounts for 10% of the dataset.
Let's say in this case that Class B represents the suspect categories, e.g. a weapon/disease/fraud has been detected. If a model scored a classification accuracy of 90% , we may decide we're happy. After all, the model appears to be correct 90% of the time.
However, this measurement is misleading when dealing with an imbalanced dataset. Another way to look at it: I could write a simple function which simply classified everything as Class A , and also achieve a classification accuracy of 90% when tested against this imbalanced dataset.
def classify_data(data):
return "Class A"
Unfortunately, my solution is useless for detecting anything meaningful in the real-world.
This is a problem.
Oversampling
One solution to this problem is to use a sampling technique to either:
- Oversample - this will create new synthetic samples that simulate the minority class to balance the dataset.
- Undersample - this will remove samples from the majority class according to some scheme to balance the dataset.
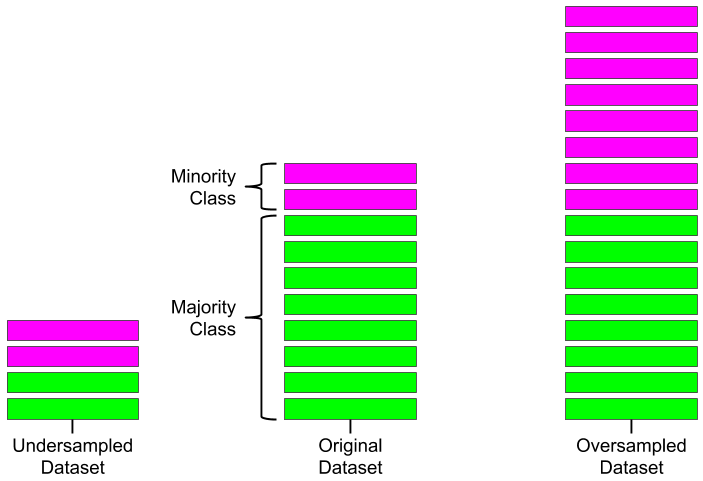
For this article we will focus on oversampling to create a balanced training set for a machine learning algorithm. Because this involves creating synthetic samples, it is important not to include these in the test set. Testing of a model must rely entirely on the real data.
It's also important to note that oversampling is not always a suitable solution to the imbalanced dataset problem. This depends entirely on factors such as the characteristics of the dataset, the problem domain, etc.
Coded example
Let's demonstrate the oversampling approach using a dataset and some Python libraries. We will be employing the imbalanced-learn package which contains many oversampling and under-sampling methods. A handy feature is its great compatibility with scikit-learn. Specifically, we will be using the Adaptive Synthetic (ADASYN) over-sampling method based on the publication below, but other popular methods, e.g. the Synthetic Minority Oversampling Technique (SMOTE), may work just as well.
He, Haibo, Yang Bai, Edwardo A. Garcia, and Shutao Li. “ADASYN: Adaptive synthetic sampling approach for imbalanced learning,” In IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), pp. 1322-1328, 2008.
First we begin by importing our packages. We have the usual suspects, numpy, matplotlib , and scikit-learn , with the addition of the new package which contains implementations of sampling methods: imblearn. If you're using a pre-configured environment, e.g. Kaggle Kernels, Anaconda, or various Docker images, then it is likely you will need to install imblearn before you can import it.
import numpy as np
import pandas as pd
import seaborn as sns
from imblearn.over_sampling import ADASYN
from numpy import genfromtxt
from sklearn.decomposition import PCA
Moving forward we will need to load in our dataset. For this example, we have a CSV file, acidosis.csv which contains our input variables, and the correct/desired classification labels.
data = pd.read_csv("acidosis.csv")
The quick invocation of the head() function gives us some idea about the form of the data, with input variables Accelerations to Median , with the final column labelled Class:
data.head()
| Accelerations | Decelerations | Prolonged Accelerations | Late Decelerations | Contractions | Light Decelerations | Severe Decelerations | Prolonged Decelerations | Variability | Width | Min | Max | Peaks | Mode | Mean | Median | Class | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 143.0 | 171.0 | 0.0 | 64.0 | 286.0 | 171.0 | 0.0 | 0.0 | 93.025 | 94.0 | 104.0 | 198.0 | 4.0 | 143.0 | 144.596681 | 144.0 | 1 |
| 1 | 96.0 | 88.0 | 0.0 | 45.0 | 169.0 | 88.0 | 0.0 | 0.0 | 102.775 | 103.0 | 103.0 | 206.0 | 0.0 | 126.0 | 130.107717 | 128.0 | 1 |
| 2 | 75.0 | 86.0 | 0.0 | 39.0 | 167.0 | 86.0 | 0.0 | 0.0 | 102.725 | 103.0 | 101.0 | 204.0 | 3.0 | 126.0 | 133.500685 | 131.0 | 1 |
| 3 | 54.0 | 58.0 | 0.0 | 17.0 | 112.0 | 58.0 | 0.0 | 0.0 | 87.025 | 87.0 | 111.0 | 198.0 | 0.0 | 143.0 | 138.734131 | 139.0 | 1 |
| 4 | 53.0 | 48.0 | 0.0 | 14.0 | 123.0 | 48.0 | 0.0 | 0.0 | 97.200 | 100.0 | 102.0 | 202.0 | 1.0 | 127.0 | 129.305465 | 128.0 | 1 |
Confirming the balance of the dataset
Before we decide if the dataset needs oversampling, we need to investigate the current balance of the samples according to their classification. Depending on the size and complexity of your dataset, you could get away with simply outputting the classification labels and observing the balance.
data["Class"].values
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])The output of the above tells us that there is certainly an imbalance in the dataset, where the majority class, 1 , significantly outnumbers the minority class, 0. To be sure of this, we can have a closer look using value_counts().
The output of which will be:
data["Class"].value_counts()
1 457 0 47 Name: Class, dtype: int64
As you can see, value_counts() has listed the number of instances per class, and it appears to be exactly what we were expecting. With the knowledge that one class consists of 47 samples and the other consists of 457 samples, it is clear this is an imbalanced dataset. Let's visualise this before moving on. We're going to use Principle Component Analysis (PCA) through sklearn.decomposition.PCA() to reduce the dimensionality of our input variables for easier visualisation.
pca = PCA(n_components=2)
data_2d = pd.DataFrame(pca.fit_transform(data.iloc[:, 0:16]))
The output of which will look something like:
data_2d
| 0 | 1 | |
|---|---|---|
| 0 | 113.344856 | 30.606726 |
| 1 | -56.729874 | -1.647731 |
| 2 | -66.749878 | -6.648316 |
| 3 | -141.344784 | -0.120158 |
| 4 | -140.461583 | -23.681364 |
| ... | ... | ... |
| 499 | 492.572807 | 31.919951 |
| 500 | 181.719481 | 6.636507 |
| 501 | 42.494165 | -20.360069 |
| 502 | -42.025654 | 11.381916 |
| 503 | -56.796775 | -12.704053 |
504 rows × 2 columns
The final column containing the classifications has been omitted from the transformation using pandas.DataFrame.iloc. After the transformation we will add the classification label column to the DataFrame for use in visualisations coming later. We will also name our columns for easy reference:
data_2d = pd.concat([data_2d, data["Class"]], axis=1)
data_2d.columns = ["x", "y", "class"]
This can be confirmed by outputting the DataFrame again:
data_2d
| x | y | class | |
|---|---|---|---|
| 0 | 113.344856 | 30.606726 | 1 |
| 1 | -56.729874 | -1.647731 | 1 |
| 2 | -66.749878 | -6.648316 | 1 |
| 3 | -141.344784 | -0.120158 | 1 |
| 4 | -140.461583 | -23.681364 | 1 |
| ... | ... | ... | ... |
| 499 | 492.572807 | 31.919951 | 0 |
| 500 | 181.719481 | 6.636507 | 0 |
| 501 | 42.494165 | -20.360069 | 0 |
| 502 | -42.025654 | 11.381916 | 0 |
| 503 | -56.796775 | -12.704053 | 0 |
504 rows × 3 columns
With our DataFrame in the desirable form, we can create a quick scatterplot visualisation which again confirms the imbalance of the dataset.
sns.lmplot(x="x", y="y", data=data_2d, fit_reg=False, hue="class");
ADASYN for oversampling
Using ADASYN through imblearn.over_sampling is straight-forward. An ADASYN
object is instantiated, and then the fit_resample() method is invoked with the
input variables and output classifications as the parameters:
ada = ADASYN()
X_resampled, y_resampled = ada.fit_resample(
data.iloc[:, 0:16], data["Class"]
)
The oversampled input variables have been stored in X_resampled and their
corresponding output classifications have been stored in y_resampled. Once
again, we're going to restore our data into the DataFrame form for easy
interrogation and visualisation:
data_oversampled = pd.concat(
[pd.DataFrame(X_resampled), pd.DataFrame(y_resampled)], axis=1
)
data_oversampled.columns = data.columns
Using value_counts() we can have a look at the new balance:
data_oversampled["Class"].value_counts()
1 457 0 455 Name: Class, dtype: int64
Now we have our oversampled and more balanced dataset. Let's visualise this on a scatterplot using our earlier approach.
data_2d_oversampled = pd.DataFrame(
pca.transform(data_oversampled.iloc[:, 0:16])
)
data_2d_oversampled = pd.concat(
[data_2d_oversampled, data_oversampled["Class"]], axis=1
)
data_2d_oversampled.columns = ["x", "y", "class"]
Similar to the last time, we've used PCA to reduce the dimensionality of our newly oversampled dataset for easier visualisation We've also restored the data into a DataFrame with the desired column names. If we plot this data, we can see there is no longer a significant majority class:
sns.lmplot(
x="x", y="y", data=data_2d_oversampled, fit_reg=False, hue="class"
);
Conclusion
In this article we've had a quick look at the problem of imbalanced datasets and suggested one approach to the problem through oversampling. We've implemented a coded example which applied ADASYN to an imbalanced dataset and visualised the difference before and after. If you plan to use this approach in practice, don't forget to first split your data into the training and testing sets before applying oversampling techniques to the training set only.
